Operasi Vektor dan Contoh Soalnya

 Pengertian

Vektor adalah segmen garis yang memiliki nilai dan mempunyai arah, penggunaan tanda (–) negatif pada nilai vektor akan berpengaruh pada arah vektor. Contohnya, vektor yang dinyatakan dengan nilai positif ke arah kanan. Begitu pun sebaliknya, vektor dengan arah ke kiri akan mempunyai nilai (–) negatif. Simbol vektor biasanya berupa ruas garis dengan anak panah pada salah satu ujungnya. 

Operasi Aljabar Vektor

Penjumlahan dan Pengurangan Vektor

Sumber: Dokumentasi Penulis

Perhatikanlah gambar vektor a, b, dan c pada koordinat Cartesius berikut ini!
Untuk a dan b vektor-vektor pada dua dimensi, berlaku :

Sumber: Dokumentasi penulis

Perkalian Skalar dengan Vektor

Jika k skalar tak nol dan vektor u = (u₁, u₂ , …, u_n), maka ku = (ku₁, ku₂, …, ku_n).

Dalam perkalian skalar dengan vektor ini, jika k > 0, maka vektor ku searah dengan vektor u. Adapun jika k < 0, maka vektor ku berlawanan arah dengan vektor u.

Sumber: Dokumentasi penulis

Sifat-sifat Operasi Hitung pada Vektor

Jika a, b, dan c merupakan vektor-vektor, kemudian k dan l skalar tak nol maka berlaku hubungan berikut :

a + b = b + a (a + b) + c = a + (b + c) a + 0 = 0 + a = a a + (–a) = 0

(kl)a = k(la) k (a+b) = ka + kb (k+l)a = ka + la 1a = a

Perkalian antara Dua Vektor

Hasil kali titik (dot product)

Hasil kali titik merupakan operasi antara dua buah vektor pada ruang yang sama, yaitu ruang yang menghasilkan skalar. Jika v dan w vektor pada ruang/dimensi yang sama, θ sudut diantara v dan w, maka hasil kali titik antara dua vektor :

Sumber: Dokumentasi penulis

Beberapa sifat perkalian titik adalah:

a · b = b · a

a · (b + c ) = (a · b )+ (a · c )

k(a · b ) = ka · b = a · kb, dimana k ∈ R

Proyeksi Ortogonal

Vektor ortogonal adalah vektor-vektor yang tegak lurus, v · w = 0 dimana harus ada referensi suatu vektor lain, misal a. Menguraikan u menjadi 2 bagian yaitu sejajar dengan suatu vektor a dan tegak lurus terhadap vektor a.

Sumber: Dokumentasi penulis

Hasil Kali Silang (cross product)

Hasil kali silang merupakan operasi antara dua vektor pada ruang tiga dimensi yang menghasilkan vektor yang tegak lurus terhadap kedua vektor yang dikalikan tersebut.

Sumber: Dokumentasi penulis

Sumber: Dokumentasi penulis

Cara menghitung :

Sumber: Dokumentasi penulis

Contoh soal

1.   Jika vektor c = (8, 9) dan d = (7, 3), tentukanlah operasi vektor berikut:
     c + d                     
     c – d
     a. (15,13) dan (1,4)

     b. (15,11) dan (7,4)

     c. (15,12) dan (1,4)

     d. (15,13) dan (7,4)

     e. (15,12) dan (8,4)

     Penyelesaian:
     c + d = (8, 9) + (7, 3) = (15, 12)
     c – d = (8, 9) – (7, 3) = (1, 4)
     Jadi operasi vektor c + d dan c – d berturut-turut adalah (15, 12) dan (1, 4).

Jadi, jawabannya adalah c. (15,12) dan (1,4)

2.   Jika titik-titik A, B, dan C segaris maka vektor  dan vektor  bisa searah atau berlainan arah.Sehingga akan ada bilangan m yang merupakan sebuah kelipatan dan membentuk persamaan...

       a. 24

       b. 25

       c. 34

       d. 35

       e. 36

       Jika B berada diantara titik A dan C, diperoleh:

       sehingga:

       Maka kelipatan m dalam persamaan:

       Diperoleh:

       disimpulkan:

       p+q=10+14=24

Jadi, Jawabannya adalah a. 24

3.   Misalkan vektor  dan vektor . Jika panjang proyeksi vektor a ̅ pada  adalah 4. Maka tentukan nilai y.

     a. 9

     b. 6

     c. 0

     d. 2

     e. 7

     Pembahasan:

     Diketahui:

     Maka:

12=8+2y

y=2

     Jadi, jawabannya d. 2

Daftar Pustaka

• Yatini. 2020. "Vektor: Pengertian, Panjang, Operasi Vektor". https://tambahpinter.com/vektor-matematika/#Operasi_Aljabar_Vektor, diakses pada 11 Maret 2021 pukul 08.36 wib.
• Mulyanto, Alwin. "Vektor". https://www.studiobelajar.com/vektor/, diakses pada 11 Maret 2021 pukul 09.07 wib.

Read More

Sudut antar Vektor pada Bidang Berdimensi Dua dan Berdimensi Tiga Bersama Contoh Soalnya

Ruang Dimensi-n 

     Himpunan bilangan nyata (real) biasanya digambarkan ke dalam sebuah gambar sederhana yang disebut garis bilangan. Garis bilangan dapat dianggap sebagai grafik sederhana yang menyatakan letak suatu bilangan, di mana bilangan yang lebih besar berada di sebelah kanan bilangan yang lebih kecil. 

     Karena garis bilangan hanya memiliki satu dimensi yaitu panjang, maka himpunan bilangan real dapat dinyatakan sebagai ruang berdimensi-1. Meskipun kata „ruang‟ menunjukkan suatu tempat berdimensi-3, namun dalam matematika „ruang‟ mempunyai makna tersendiri. Berdasarkan definisinya, ruang dalam matematika merupakan himpunan dari objek-objek yang memiliki sifat yang sama dan memenuhi semua aturan yang berlaku dalam ruang tersebut. 

Definisi Ruang-1 atau 𝑅 1 

     Ruang dimensi-1 atau ruang-1 (𝑅 1 ) adalah himpunan semua bilangan real (ℝ). Himpunan bilangan real dapat digambarkan oleh garis bilangan real : 

     Jadi, garis bilangan berfungsi untuk menunjukkan letak suatu titik pada suatu garis berdasarkan besarnya. Gagasan ini memunculkan gagasan berikutnya bahwa suatu titik dapat berada pada suatu bidang ataupun ruang. Pada pertengahan abad ke-17 lahirlah konsep ruang dimensi-2 dan dimensi-3, yang kemudian pada akhir abad ke-19 para ahli matematika dan fisika memperluas gagasannya hingga ruang dimensi-n. -3 -2 -1 0 1 2 3 Bulat Negatif Nol Bulat Positif Bil. Rasional & irasional.

Definisi Ruang-2 atau 𝑅 2

     Ruang dimensi-2 atau ruang-2 (𝑅 2 ) adalah himpunan pasangan bilangan berurutan (𝑥, 𝑦), di mana x dan y adalah bilangan-bilangan real. Pasangan bilangan (𝑥,𝑦) dinamakan titik (point) dalam 𝑅 2 , misal suatu titik P dapat ditulis 𝑃(𝑥, 𝑦). Bilangan x dan y disebut koordinat dari titik P. 

     Untuk menggambarkan titik-titik di 𝑅 2 secara geometris, koordinat x dan y dianggap berada pada dua garis bilangan yang berbeda yang membentuk suatu sistem koordinat. Garis bilangan tersebut dinamakan sumbu koordinat. Sumbu koordinat tersebut digambarkan saling tegak lurus dan membentuk suatu sistem yang disebut sistem koordinat siku-siku. Pada 𝑅 2 sistem ini dinamakan sistem koordinat-xy atau sistem koordinat kartesius (Cartesian system) yang dibangun oleh : 

• Sumbu x (x-axis) yaitu garis tempat semua titik yang mempunyai koordinat (x, 0). 
• Sumbu y (y-axis) yaitu garis tempat semua titik yang mempunyai koordinat (0, y).

     Suatu titik yang berada tepat di kedua sumbu dinamakan titik asal (origin point) ditulis O(0, 0). Titik ini adalah titik di mana sumbu x dan y saling berpotongan. 

Definisi Ruang-3 atau 𝑅 3 

     Ruang dimensi-3 atau ruang-3 (𝑅 3 ) adalah himpunan tripel bilangan berurutan (𝑥, 𝑦, 𝑧), di mana x, y, dan z adalah bilangan-bilangan real. Tripel bilangan (𝑥, 𝑦, 𝑧) dinamakan titik (point) dalam 𝑅 3 , misal suatu titik P dapat ditulis 𝑃(𝑥, 𝑦, 𝑧). Bilangan x, y, dan z, disebut koordinat dari titik P.

     Seperti halnya 𝑅 2 , 𝑅 3 memiliki sistem koordinat siku-siku yaitu sistem koordinat-xyz, dengan titik asal 𝑂 0,0, 0 , yang dibangun oleh : 

• Sumbu x (x-axis) yaitu garis tempat semua titik yang mempunyai koordinat (𝑥,0, 0). y x O
• Sumbu y (y-axis) yaitu garis tempat semua titik yang mempunyai koordinat (0,𝑦, 0). 
• Sumbu z (z-axis) yaitu garis tempat semua titik yang mempunyai koordinat (0,0, 𝑧).

     Menjelang akhir abad 19, para matematikawan dan fisikawan mulai menemukan gagasan bahwa dimensi tidak hanya terbatas pada dimensi-3 dengan tripel bilangannya, tetapi juga kuadrupel sebagai titik pada ruang dimensi-4, kuintupel pada ruang dimensi-5, dan seterusnya. Hal ini menghasilkan generalisasi untuk ruang dimensi-n. 

Definisi tupel-n-berurutan 

     Jika n adalah sebuah bilangan positif, maka tupel-n-berurutan (ordered-n-tuple) adalah sebuah urutan n buah bilangan real (𝑎1 , 𝑎2 , . . . , 𝑎𝑛 ). 

Definisi Ruang-n atau 𝑅 𝑛 

     Ruang dimensi-n atau ruang-n (𝑅 𝑛 ) adalah himpunan semua tupel-n-berurutan (𝑎1 ,𝑎2 , . . . , 𝑎𝑛 ), dengan 𝑎1 , 𝑎2 , . . . , dan 𝑎𝑛 adalah bilangan-bilangan real. Tupel-n bilangan 𝑎1 ,𝑎2 , . . . , 𝑎𝑛 dinamakan titik (point) dalam 𝑅 𝑛 , misal suatu titik P dapat ditulis 𝑃(𝑎1 , 𝑎2 , . . . , 𝑎𝑛 ). Bilangan 𝑎1 , 𝑎2 , . . . , dan 𝑎𝑛 disebut koordinat dari P. 

     Jelas bahwa ruang dimensi-n dengan n > 3 tidak dapat divisualisasikan secara geometris, namun penemuan ini sangat berguna dalam pekerjaan analitik dan numerik, karena tidak sedikit permasalahan nyata tidak dapat divisualisasikan dengan grafis namun memerlukan penalaran dan penyelesaian secara matematis. 

     𝑅 𝑛 yang merupakan generalisasi dari 𝑅 1 , 𝑅 2 , dan 𝑅 3 , menyebabkan sifat-sifat dan aturan-aturan di dalamnya adalah sama, perbedaannya hanya terletak pada ukuran atau banyak komponen yang akan dihitung. Walaupun bab ini hanya menyajikan definisi, teorema, atau sifat-sifat dalam 𝑅 2 dan 𝑅 3 , tetapi semuanya akan berlaku untuk 𝑅 𝑛 , setelah dimodifikasi sesuai dimensinya. Seperti definisi jarak antar dua titik dalam 𝑅 2 dan 𝑅 3 berikut yang dapat digeneralisasi untuk 𝑅 𝑛 . 

Vektor 

     Banyak kuantitas fisis, seperti luas, panjang, massa, suhu, dan lainnya, dapat dijelaskan secara lengkap hanya dari besarnya, misalnya 50 kg, 100 m, 30 ℃, dll. Kuantitas fisis ini dinamakan skalar. Dalam matematika, skalar mengacu pada semua bilangan yang bersifat konstan. 

     Namun, ada kuantitas fisis lain yang tidak hanya memiliki besar/nilai tapi juga arah, seperti kecepatan, gaya, pergeseran, dan lain-lain. Kuantitas fisis ini dalam fisika maupun matematika dinamakan vektor. Dalam matematika, ilmu vektor menjadi salah satu cabang ilmu yang semakin luas perkembangannya serta penerapannya, dan tidak terbatas pada mempelajari besaran-besaran yang memiliki nilai dan arah tetapi sebagai suatu besaran yang memiliki banyak komponen yang membentuk satu kesatuan dari besaran itu sendiri. 

Notasi Vektor 

     Vektor biasanya dinyatakan dengan huruf kecil tebal (a), atau diberi tanda panah di atasnya (𝑎 ), atau tanda garis bawah ( 𝑎 ). 

Definisi Vektor 

     Sebuah vektor a dengan komponen-n (berdimensi-n) di dalam 𝑅 𝑛 adalah suatu aturan tupel-n dari bilangan-bilangan yang ditulis sebagai baris (𝑎1 ,𝑎2 , … , 𝑎𝑛 ) atau sebagai kolom 𝑎1 𝑎2 ⋮ 𝑎𝑛 , dengan 𝑎1 ,𝑎2 , … , 𝑎𝑛 adalah bilangan-bilangan real dan dinamakan komponen dari vektor a. Dengan demikian, di 𝑅 2 vektor dapat ditulis : 𝐚 = (𝑎1 , 𝑎2 ) atau 𝐚 = 𝑎1 𝑎2 , dan di 𝑅 3 vektor dapat ditulis : 𝐚 = (𝑎1 ,𝑎2 , 𝑎3 ) atau 𝐚 = 𝑎1 𝑎2 𝑎3 . Pada bagian berikutnya, vektor akan sering disajikan dalam bentuk baris (vektor baris). Berdasarkan definisi titik dan vektor, simbol (𝑎1 , 𝑎2 , …, 𝑎𝑛 ) mempunyai dua tafsiran geometrik yang berbeda, yaitu sebagai titik dalam hal 𝑎1 , 𝑎2 , …, 𝑎𝑛 adalah koordinat, dan sebagai vektor dalam hal 𝑎1 ,𝑎2 , … , 𝑎𝑛 adalah komponen.

Teorema : Sudut Antara Dua Vektor 

     Jika u dan v adalah vektor-vektor tak nol, dan 𝜃 adalah besar sudut di antara kedua vektor tersebut, maka 

• 𝜃 lancip (0° < 𝜃 < 90°) jika dan hanya jika 𝐮 ∙ 𝐯 > 0 
• 𝜃 tumpul (90° < 𝜃 < 180°) jika dan hanya jika 𝐮 ∙ 𝐯 < 0 
• 𝜃 siku-siku (𝜃 = 90°) jika dan hanya jika 𝐮 ∙ 𝐯 = 0 

     Dua vektor yang membentuk sudut siku-siku dinamakan ortogonal (tegak lurus). 

Teorema : Sifat-sifat Perkalian Titik 

     Jika u, v, dan w adalah vektor- vektor di 𝑅 2 atau 𝑅 3 dan k adalah skalar, maka 

     a. 𝐮 ∙ 𝐯 = 𝐯 ∙ 𝐮 

     b. 𝐮 ∙ 𝐯 + 𝐰 = 𝐮 ∙ 𝐯 + 𝐮 ∙ 𝐰 

     c. 𝑘 𝐮 ∙ 𝐯 = 𝑘𝐮 ∙ 𝐯 = 𝐮 ∙ (𝑘𝐯) 

     d. 𝐯 ∙ 𝐯 > 0 jika 𝐯 ≠ 𝟎 dan 𝐯 ∙ 𝐯 = 0 jika 𝐯 = 𝟎 

Proyeksi 

     Dua vektor yang titik asalnya berimpit dapat menghasilkan vektor lain yang dinamakan vektor proyeksi. Perhatikan ilustrasi berikut. 

     Misalkan a dan b berimpit di titik asalnya. Jika dari titik ujung b ditarik garis menuju a sedemikian sehingga tegak lurus a (diproyeksikan terhadap a), maka vektor yang dapat dibuat dengan titik asal yang sama dan berujung di titik di mana b diproyeksikan pada a dinamakan vektor proyeksi b terhadap a. Vektor ini disebut juga proyeksi ortogonal b pada a. 

     Dengan cara yang sama dapat diperoleh vektor proyeksi a terhadap b. 

Notasi Vektor Proyeksi 

     Vektor proyeksi b terhadap a dinotasikan proy𝐚 𝐛 

     Vektor proyeksi a terhadap b dinotasikan dengan proy𝐚𝐛 

Teorema : Proyeksi Ortogonal 

     Jika u dan v adalah vektor di 𝑅 2 atau 𝑅 3 dan keduanya bukan vektor nol, maka 

proy𝐚 𝐛 = 𝐚 ∙ 𝐛 𝐚 2 𝐚 dan proy𝐛 𝐚 = 𝐚 ∙ 𝐛 𝐛 2 𝐛 

     Sedangkan panjang dari vektor-vektor proyeksi tersebut adalah 

 proy𝐚 𝐛 = 𝐚 ∙ 𝐛 𝐚 dan proy𝐛 𝐚 = 𝐚 ∙ 𝐛 𝐛 

     Contoh: 

     Jika 𝐚 = (1, 0, −2) dan 𝐛 = (2,1, −1) , tentukan vektor proyeksi a pada b. Penyelesaian : 𝐚 ∙ 𝐛 = 4 dan 𝐛 2 = 6 maka proyeksi ortogonal a pada b adalah 

proy𝐛 𝐚 = 𝐚 ∙ 𝐛 𝐛 2 𝐛 = 4 6 2,1, −1 = 4 3 , 2 3 , − 2 3 ∎ 

Perkalian Silang (Cross Product) 

     Berikut akan diperkenalkan sebuah operasi antar vektor dalam 𝑅 3 . Jika perkalian titik akan menghasilkan skalar/bilangan, maka perkalian silang akan menghasilkan vektor. Dan jika proyeksi ortogonal suatu vektor terhadap vektor la in akan menghasilkan vektor baru yang berimpit dengan vektor tersebut, maka perkalian silang dua vektor akan menghasilkan vektor baru yang tegak lurus dengan kedua vektor tersebut. 

Definisi Perkalian Silang 

     Jika 𝐮 = (𝑢1 ,𝑢2 ,𝑢3 ) dan 𝐯 = (𝑣1 , 𝑣2 , 𝑣3 ) adalah vektor di 𝑅 3 , maka perkalian silang 𝐮 × 𝐯 didefinisikan oleh 

𝐮 × 𝐯 = (𝑢2𝑣3 − 𝑢3𝑣2 , 𝑢3𝑣1 − 𝑢1𝑣3 ,𝑢1𝑣2 − 𝑢2𝑣1 ) 

     atau dalam notasi determinan 

𝐮 × 𝐯 = 𝑢2 𝑢3 𝑣2 𝑣3 , − 𝑢1 𝑢3 𝑣1 𝑣3 , 𝑢1 𝑢2 𝑣1 𝑣2 

     Rumus di atas dapat dibuat pola yang mudah diingat. Bentuklah matriks 2 × 3 : 

 𝑢1 𝑢2 𝑢3 𝑣1 𝑣2 𝑣3 

     Komponen pertama dari 𝐮 × 𝐯 adalah determinan matriks tersebut setelah kolom pertama dicoret, komponen ke-2 adalah negatif dari determinan matriks setelah kolom ke-2 dicoret, dan komponen ke-3 adalah determinan matriks setelah kolom ke-3 dicoret. 

     Contoh: 

     Misalkan 𝐮 = (1, 2,−2) dan 𝐯 = (3, 0, 1), maka 

 1 2 −2 3 0 1 

 𝐮 × 𝐯 = 2 −2 0 1 , − 1 −2 3 1 , 1 2 3 0 = 2, −7,−6 ∎ 

     Secara geometris, perkalian silang 𝐮 × 𝐯 dapat diinterpretasikn oleh gambar berikut, 

     Arah 𝐮 × 𝐯 dapat ditentukan dengan “aturan tangan kanan” (right hand rule). Misalkan 𝜃 adalah sudut di antara u dan v, dan anggaplah u terotasi sejauh sudut 𝜃 menuju v (sehingga berimpit dengan v). Jika jari-jari tangan kanan menunjukkan arah rotasi u maka ibu jari menunjukkan arah 𝐮 × 𝐯. 

     Dengan menggunakan definisi ataupun dengan mempraktekkan aturan ini, dapat diperoleh hasil-hasil berikut : 

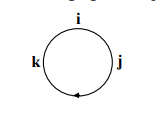
𝐢 × 𝐢 = 𝐣 × 𝐣 = 𝐤 × 𝐤 = 𝟎 

𝐢 × 𝐣 = 𝐤 , 𝐣 × 𝐤 = 𝐢 , 𝐤 × 𝐢 = 𝐣 

𝐣 × 𝐢 = −𝐤 , 𝐤 × 𝐣 = −𝐢 , 𝐢 × 𝐤 = −𝐣 

     Diagram berikut dapat membantu untuk mengingat hasil perkalian di atas. 

     Perkalian silang 𝐮 × 𝐯 dapat dinyatakan secara simbolis dalam bentuk determinan 3 × 3 : 

𝐮 × 𝐯 = 𝐢 𝐣 𝐤 𝑢1 𝑢2 𝑢3 𝑣1 𝑣2 𝑣3 = 𝑢2 𝑢3 𝑣2 𝑣3 𝐢 − 𝑢1 𝑢3 𝑣1 𝑣3 𝐣 + 𝑢1 𝑢2 𝑣1 𝑣2 𝐤  

     Contoh: 

     Contoh 1dapat dikejakan dengan cara : 

𝐮 × 𝐯 = 𝐢 𝐣 𝐤 1 2 −2 3 0 1 = 2 −2 0 1 𝐢 − 1 −2 3 1 𝐣 + 1 2 3 0 𝐤 = 2𝐢 − 7𝐣 − 6𝐤 ∎ 

Teorema : Hubungan Perkalian Silang dan Perkalian titik 

     Jika u dan v adalah vektor di 𝑅 3 , maka : 

     a. 𝐮 ∙ 𝐮 × 𝐯 = 0 ( 𝐮 × 𝐯 ortogonal ke u ) 

     b. 𝐯 ∙ 𝐮 × 𝐯 = 0 ( 𝐮 × 𝐯 ortogonal ke u ) 

     c. 𝐮 × 𝐯 𝟐 = 𝐮 𝟐 𝐯 𝟐 − 𝐮 ∙ 𝐯 𝟐 (Identitas Lagrange/Lagrange Identity) 

Teorema : Sifat-Sifat Perkalian Silang 

     Jika u, v, dan w dalah sebarang vektor di 𝑅 3 ddan k adalah sebarang skalar, maka : 

     a. 𝐮 × 𝐯 = − 𝐯 × 𝐮 

     b. 𝐮 × 𝐯+ 𝐰 = 𝐮 × 𝐯 + (𝐮 × 𝐰) 

     c. 𝐮 + 𝐯 × 𝐰 = 𝐮 × 𝐰 + (𝐯 × 𝐰) 

     d. 𝑘 𝐮 × 𝐯 = 𝑘𝐮 × 𝐯 = 𝐮 × (𝑘𝐯) 

     e. 𝐮 × 𝟎 = 𝟎 × 𝐮 = 𝟎 

     f. 𝐮 × 𝐮 = 𝟎 

     g. 𝐮 ∙ 𝐯 × 𝐰 = 𝐮 × 𝐯 ∙ 𝐰 = 𝑢1 𝑢2 𝑢3 𝑣1 𝑣2 𝑣3 𝑤1 𝑤2 𝑤3 

      Berdasarkan teorema-teorema sebelumnya, dapat diturunkan teorema berikut. 

Teorema : Aplikasi Geometri Perkalian Silang 

     Jika u, v, dan w vektor-vektor di 𝑅 3 dengan titik asal yang sama, maka 

     a. Jika 𝜃 adalah sudut di antara u dan v, maka 𝐮 × 𝐯 = 𝐮 𝐯 sin 𝜃 

     b. Norma dari 𝐮 × 𝐯 sama dengan luas jajaran genjang yang dibentuk oleh u dan v, atau Luas jajar genjang = 𝐮 × 𝐯 

     c. Volume bangun yang dibentuk oleh ketiganya adalah 𝑎𝑏𝑠[𝐮 ∙ 𝐯 × 𝐰 ]. 

     Contoh: 

     a, b, dan c adalah sebarang vektor di 𝑅 3 yang berimpit di titik awalnya. Jika ketiganya dihubungkan akan membentuk suatu bangun dimensi-3 (parallelpiped).

     Luas masing-masing sisinya adalah : 

 𝐚 × 𝐛 , 𝐛 × 𝐜 , 𝐚 × 𝐜 

     Sedangkan volume bangun tersebut adalah : 

𝑎𝑏𝑠(𝐚 ∙ 𝐛 × 𝐜 ) 

     Rumus volume di atas biasanya digunakan untuk mengetahui apakah ketiga vektor berada pada bidang yang sama. Jika volume yang dihitung bernilai nol, maka ketiganya berada pada bidang yang sama, dan sebaliknya jika volumenya tidak sama dengan nol. Fungsi abs(absolute)/mutlak berguna untuk mempositifkan hasil akhir perhitungan volume. 

     Contoh: 

     Tentukan apakah ketiga vektor 𝐚 = (1, 4, −7), 𝐛 = (2,−1, 4), dan 𝐜 = (0,−9, 18) terletak pada satu bidang di 𝑅 3 atau tidak. 

     Penyelesaian : 

𝐚 ∙ 𝐛 × 𝐜 = 1 4 −7 2 −1 4 0 −9 18 1 4 2 −1 0 −9 = 1 −1 18 + 4 4 0 + −7 2 −9 — { 7 −1 0 + 1 4 −9 + 4 2 18 } = −18 + 126 − 144 + 36 = 0 

     Jadi, ketiga vektor tersebut terletak pada satu bidang di 𝑅 3 ∎ 

     

Daftar Pustaka:

• Rivership, Mkls. 2014. "Vektor Ruang 2 dan 3 (vector 2D & 3D)", https://www.slideshare.net/mklsrivership/vektor-diruang-2dan3-121002010325phpapp01?from_action=save, diakses pada 5 Maret 2021 pukul 07.50 wib. 

Read More

Menjelajahi Keindahan Alam Indonesia

Indonesia terkenal di mancanegara sebagai negara dengan alam yang indah. Negara kepulauan seluas 1,91 juta km2 ini memang memiliki bentang alam yang memesona, mulai dari Aceh hingga Papua. Tak heran jika jumlah wisatawan yang datang terus bertambah, baik dari dalam maupun luar negeri untuk melihat langsung ragam keindahan wisata alam yang ada di Indonesia.

Karena keindahan alam Indonesia yang tak terkira, berlibur pun tak perlu jauh-jauh ke luar negeri. Ada sejumlah destinasi wisata alam Indonesia yang sangat menarik untuk dikunjungi. Apa saja di antaranya? Berikut rekomendasi keindahan alam Indonesia terbaik yang telah mendunia:

Menjelajahi Keindahan Alam Indonesia

1. Pulau Weh

Pulau Weh | Sumber gambar: Stingynomads.com

Pulau Weh menyandang status sebagai daerah paling barat di wilayah Indonesia. Di pulau inilah kamu dapat menemukan Tugu Nol Kilometer sebagai simbol awal perjalanan di wilayah Indonesia. Meskipun tidak terlalu besar, Pulau Weh memiliki keindahan alam khas Nusantara yang luar biasa. Untuk mencapai pulau ini, kamu harus berlayar dengan kapal feri sekitar 2 jam perjalanan.

Salah satu spot yang menunjukkan keindahan alam Indonesia di Pulau Weh adalah Pantai Iboih. Pantai ini terkenal dengan panoramanya yang sangat indah. Air laut yang membentang tampak biru jernih. Pasir di sepanjang pesisir pantai pun terlihat putih dan lembut. Selain Pantai Iboih, ada pula beberapa pantai lain, seperti Pantai Kasih, Pantai Tapak Gajah, Pantai Sumur Tiga, dan Pantai Anoi Itam, yang tak kalah memesona.

2. Danau Toba

Danau Toba | Sumber gambar: maritim.go.id

Keindahan alam Indonesia juga dapat kamu nikmati saat berkunjung ke Danau Toba yang terletak di wilayah Sumatera Utara. Danau Toba merupakan danau terbesar di Indonesia. Di tengah-tengah danau ini, ada sebuah daratan yang cukup luas yaitu Pulau Samosir. Kamu bisa berkunjung ke Pulau Samosir dengan menumpang kapal feri selama 30 menit. Di Pulau Samosir, kamu bisa mengeksplorasi sejarah dan kebudayaan masyarakat lokal.

Berada sekitar 900 meter dari permukaan laut, suasana di sekitar Danau Toba terasa sejuk. Sembari bersantai menikmati panorama alam yang memesona, cicipi kuliner olahan seafood yang segar. Jangan lupa memilih spot terbaik untuk menyaksikan keelokan Danau Toba yang sempurna. Jika ingin lebih puas menjelajah objek wisata alam Indonesia ini, carilah penginapan terdekat.

3. Belitung

Pulau Belitung | Sumber gambar: belitunginfo.com

Pulau Belitung menjadi salah satu destinasi wisata yang menunjukkan keindahan alam Indonesia. Pengunjung yang datang ke daerah ini terus meningkat sepanjang tahun. Ada sejumlah spot yang menawarkan keindahan alam di Pulau Belitung, di antaranya Tanjung Binga, Pulau Leebong, Pantai Tanjung Kelayang, dan Pulau Lengkuas. Tempat-tempat ini identik dengan pasir putih dan air laut yang jernih.

Nama Pulau Belitung semakin terkenal sejak Andrea Hirata mempublikasikan novelnya berjudul Laskar Pelangi. Berlatar belakang keindahan Pulau Lengkuas yang memukau, kisah inspiratif ini berhasil menarik minat banyak orang untuk datang ke Belitung. Nah, bagi kamu yang berencana berlibur ke pulau ini, sediakan waktu lebih dari satu atau dua hari untuk menjelajahinya.

4. Gunung Bromo

Gunung Bromo | Sumber gambar: tribunnewswiki.com

Gunung Bromo adalah salah satu gunung yang sangat populer di kalangan wisatawan karena menawarkan keindahan alam Indonesia yang menakjubkan. Meskipun berstatus sebagai gunung berapi aktif, Bromo tidak pernah sepi dari pengunjung.

Ada sejumlah spot menarik di sekitar kawasan Gunung Bromo yang menjadi favorit wisatawan. Salah satunya, Puncak Penanjakan yang kerap menjadi lokasi untuk menyaksikan panorama matahari terbit. Puncak Penanjakan telah dilengkapi dengan berbagai fasilitas, mulai dari toilet, Mushola, hingga kios makanan.

Selain Puncak Penanjakan, kamu juga wajib berkunjung ke Pasir Berbisik. Ini adalah hamparan padang pasir seluas 5.920 hektare yang terletak di jalur menuju puncak Bromo. Tekstur pasirnya halus dan berwarna hitam. Pemandangan alam di tempat ini terlihat semakin eksotis dengan keberadaan tebing-tebing megah di sekitarnya.

5. Bunaken

Taman Nasional Bunaken | Sumber gambar: cahayasiang.com

Salah satu bukti keindahan alam Indonesia bisa kamu temukan di Bunaken. Taman Nasional Bunaken terletak di Sulawesi Utara, tepatnya di Segitiga Terumbu Karang. Di kawasan ini, ada sekitar 390 spesies terumbu karang serta berbagai jenis ikan dan hewan laut. Tak heran jika banyak wisatawan datang ke Taman Laut Bunaken demi bisa menyaksikan habitat bawah laut ini dari dekat.

Aktivitas favorit selama berada di Taman Laut Bunaken adalah diving dan snorkeling. Bahkan, Bunaken disebut-sebut sebagai destinasi wisata menyelam terbaik di Indonesia. Spot yang paling disukai adalah Bunaken Timur Mandolin dan Puncak Barakuda. Menyaksikan keindahan suasana di tempat ini akan membuat kamu terpukau. Jika tak ingin basah-basahan, manfaatkan fasilitas berupa perahu semi selam dengan dinding kaca.

6. Pantai Sanur

Pantai Sanur | Sumber gambar: water-sport-bali.com

Jika berbicara tentang keindahan alam Indonesia, Bali tak bisa diabaikan begitu saja. Bahkan, nama pulau ini lebih akrab bagi para wisatawan mancanegara karena pemandangannya yang eksotis. Pantai Sanur terletak di timur Kota Denpasar sehingga menjadi lokasi yang sangat ideal untuk menyaksikan keindahan matahari terbit.

Bagi kamu yang berlibur ke Pantai Sanur, nikmati juga keseruan bermain pasir dan air atau berenang. Kontur pesisir pantai ini memang landai dan sangat bersahabat bagi pengunjung. Ombaknya juga tidak terlalu kencang. Selain itu, kamu juga bisa menyewa kano untuk menikmati panorama lautan yang indah pada sore hari.

7. Raja Ampat

Raja Ampat | Sumber gambar: infonusantara.id

Jika memiliki budget liburan yang cukup besar, jangan ragu untuk memilih Raja Ampat sebagai destinasi wisata alam di Indonesia. Kamu tidak akan kecewa menyaksikan keindahan alam Indonesia yang masih permai dan alami ini. Meskipun cukup jauh di wilayah timur Indonesia, Raja Ampat selalu menjadi primadona bagi para wisatawan. Fasilitas yang tersedia di kawasan wisata ini pun sudah cukup lengkap dan nyaman.

Salah satu tempat menarik di Raja Ampat adalah Pianemo atau Painemu yang merupakan kawasan karst. Gugusan pulau karang ini tampak cantik membentang di laut sehingga sering dijuluki “surga kecil” di Tanah Papua. Ada juga yang disebut Laguna Bintang, yaitu laguna yang berbentuk seperti bintang dan memiliki air berwarna hijau toska. Laguna yang terbentuk secara alami ini bisa dinikmati secara utuh dari puncak bukit.

Berkunjung ke Raja Ampat juga tidak akan lengkap jika belum menginjakkan kaki di Arborek. Ini adalah sebuah pulau kecil di Raja Ampat yang memiliki pantai landai dengan arus air yang tenang. Hamparan pasir berwarna putih berpadu dengan pepohonan kelapa menciptakan suasana yang sangat eksotis.

8. Wae Rebo

Desa Wae Rebo | Sumber gambar: travel.kompas.com

Berada di ketinggian 1.500 meter dari permukaan laut, Desa Wae Rebo kerap mendapatkan julukan negeri di atas awan. Meskipun tak mudah untuk mencapati Desa yang berlokasi di Manggarai, Nusa Tenggara Timur ini, namun beratnya perjalanan tersebut akan terbayarkan lunas setelah kamu melihat langsung indahnya panorama bangunan-bangunan tradisional khas Wae Rebo berbingkai alam asri dan gunung-gunung megah sebagai latar belakangnya.

Memiliki nilai budaya dan sejarah yang panjang, Wae Rebo telah dinobatkan sebagai salah satu situs warisan dunia UNESCO pada 2012 silam.

9. Pulau Komodo

Pulau Komodo | Sumber gambar: travel.detik.com

Satu lagi keindahan alam Indonesia yang telah mendunia di Nusa Tenggara Timur, yakni Pulau Komodo. Di destinasi wisata alam Indonesia satu inilah hidup tak kurang dari 2000 ekor Komodo, hewan endemik Indonesia yang juga telah populer di mata dunia.

Namun, daya tarik dari pulau Komodo tak hanya pada hewan reptil purba-nya saja, melainkan juga keindahan alamnya yang sangat memukau!

10. Wakatobi

Wakatobi | Sumber gambar: potensilokal.com

Berada di Sulawesi Tenggara, Taman Nasional Wakatobi yang sebagian besar wilayahnya merupakan perairan ini merupakan destinasi wisata alam yang menawarkan keindahan alam Indonesia yang sangat menakjubkan.

Kerap dijuluki sebagai surga bawah laut, destinasi wisata alam di Indonesia ini merupakan rumah bagi berbagai jenis flora dan fauna laut termasuk gugusan karang indah nan eksotis yang dikonservasi di sini. Mampir ke sini, sempatkan diri untuk diving atau snorkeling untuk lihat lebih dekat keindahan alam bawah laut Indonesia.

11. Banda Neira

Banda Neira | Sumber gambar: idntimes.com

Wilayah timur Indonesia memang banyak menyimpan pesona keindahan alam yang sangat menakjubkan. Salah satunya bisa kamu temukan di Banda Neira, pulau yang terletak di Maluku Tengah.

Pulau kecil ini menjadi salah satu destinasi wisata alam di Indonesia favorit wisatawan mancanegara karena panorama alamnnya yang sangat indah. Selain keindahan alamnya, ternyata pulau ini juga menyimpan sejarah panjang Indonesia karena dahulu tempat ini merupakan salah satu pusat perdagangan pala dimasa kolonialisasi Belanda. Bahkan, kamu masi bisa menemukan sisa-sisa peninggalan Belanda ditengah-tengah asrinya alam di pulau ini.

12. Danau Sentani

Danau Sentani | Sumber gambar: pegipegi.com

Sentani memiliki arti "di sini kami tinggal dengan damai" dan sesuai dengan nama ini, suasana di Danau Sentani memang terasa sangat damai dan menenagkan. Hal ini dikarenakan panorama danau terbesar di Papua masih sangat asri dan juga eksotis.

Memiliki luas 9.360 hektar dan berada di ketinggian 75 meter dari permukaan laut destinasi wisata alam Indonesia ini memiliki atmosfer udara yang sangat menyegarkan.

Setiap tahunnya, tepatnya pada bulan Juni kerap diselenggarakan Festival Danau Sentani dimana kamu bisa menyaksikan berbagai pertunjukkan budaya khas Papua seperti tari perang hingga tari-tarian tradisional lainnya yang ditarikan di atas perahu sambil diiringi alat-alat musik tradisional khas Papua dengan keindahan alam Indonesia nan asri sebagai latar belakang yang membingkainya.

13. Mentawai

Mentawai | Sumber gambar: kemenkopmk.go.id

Kepulauan Mentawai yang berada di Sumatera Barat merupakan destinasi wisata selanjutnya yang menawarkan keindahan alam Nusantara yang telah diakui dunia. Terkenal akan pantai-pantainya yang indah dan berombak, setiap tahunnya ribuan peselancar dari berbagai belahan dunia mengunjungi tempat ini untuk menaklukan ombak yang ada di kepulauan Mentawai.

Untuk kamu penggemar islands hopping dan juga wisata pantai, Kepulauan Mentawai jelas merupakan salah satu tujuan wisata alam di Indonesia dengan keindahan memukau yang sangat recommended.

14. Derawan

Derawan | Sumber gambar: wartawisata.id

Keindahan alam Indonesia terbaik selanjutnya bisa kamu temukan di gugusan kepulauan Derawan yang berada di provinsi Kalimantan Timur. Gugusan kepulauan satu terkenal sebagai salah satu destinasi diving dan snorkeling yang popularitas keindahannya telah mendunia. Salah satu titik penyelaman populer di Derawan adalah "Blue Trigger Wall" yang memiliki kedalaman mencapai sepuluh meter.

15. Kawah Ijen

Kawah Ijen | Sumber gambar: hot.liputan6.com

Jawa Timur merupakan salah satu Provinsi di Pulau Jawa yang banyak menyimpan pesona keindahan alam, salah satunya berada di Cagar Alam Taman Wisata Ijen yang berada di Banyuwangi. Destinasi wisata alam populer di Indonesia ini terkenal akan kawahnya yang mengeluarkan api berwarna kebiruan.

Berada pada ketingian 2.368 meter di atas permukaan laut, tengah malam sebelum matahari terbit adalah waktu terbaik untuk mencapai puncak dari Kawah Ijen dimana kamu bisa menyaksikan eksotisme api biru yang terdapat di kawah ini.

16. Puncak Jayawijaya

Gunung Jayawijaya | Sumber gambar: republika.go.id

Meskipun memiliki iklim tropis, terdapat satu lokasi di Indonesia yang memiliki salju, yakni Puncak Jayawijaya, puncak tertinggi di Indonesia yang ada di Papua. Tak hanya di Indonesia, Puncak Jayawijaya bahkan merupakan puncak tertinggi di Australia dan Oceania, lho.

Berada di ketinggian yang sangat ekstrem, pendakian ke puncak Jayawijaya tak hanya sangat menantang dan berbahaya namun juga menawarkan pemandangan keindahan alam Indonesia nan eksotis yang takkan bisa kamu temukan di belahan lain Nusantara.

Keindahan alam Indonesia tampak sangat mencolok di beberapa destinasi wisata ini. Namun, selain itu masih ada banyak objek wisata alam di Indonesia yang terkenal hingga ke mancanegara. Suasana yang masih natural dan alami menjadi magnet tersendiri bagi para turis. Namun, tak perlu khawatir karena fasilitas yang tersedia juga sudah cukup lengkap.

Nah, bagi yang ingin menyaksikan keindahan alam Indonesia, destinasi wisata alam Nusantara mana yang jadi pilihan favoritmu?

Daftar Pustaka:

• Yohannes, Markus. 2020. "16 Keindahan Alam Indonesia Terbaik dan Menakjubkan", https://www.traveloka.com/id-id/explore/destination/keindahan-alam-indonesia-yang-mendunia-acc/19116, diakses pada 4 Maret 2021 pukul 07.45 wib.

Read More