Vektor adalah sebuah besaran yang berarah.
Vektor juga bisa digambarkan sebagai panah yang menunjukan arah vektor dan panjang garisnya disebut juga Besar Vektor.

Vektor yang berawal dari titik A dan berakhir di titik B bisa ditulis sebagai :

atau
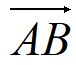
Jenis – Jenis Vektor
Vektor juga memiliki beberapa jenis tersendiri, yaitu sebagai berikut.
Vektor Posisi
Vektor Posisi adalah vektor yang titik awalnya di titik 0 (0,0) dan titik ujungnya di A (a1, a2).
Vektor 0 (Nol)
Vektor 0 adalah vektor yang panjangnya nol dan dinotasikan

Vektor nol tidak memiliki arah vektor yang jelas.
Vektor Satuan
Vektor satuan adalah vektor yang panjangnya satu satuan. Vektor satuan dari
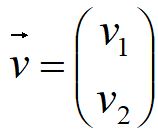
adalah

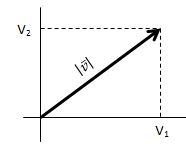
Vektor di R2
Panjang sebuah segmen garis yang menyatakan vektor atau dinotasikan sebagai Panjang vektor sebagai :

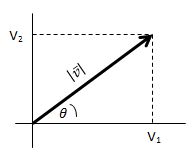
Panjang vektor tersebut ialah dapat dikaitkan dengan sudut θ yang dibentuk oleh vektor dan sumbu x positif.
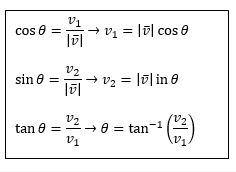
Operasi di Vektor di R2
Penjumlahan Vektor
2 vektor atau lebih dapat dijumlahkan dan hasilnya dapat disebut resultan.
Penjumlahan vektor secara aljabar dapat dilakukan dengan cara menjumlahkan komponen yang juga seletak. Jika

Maka

Secara grafis, penjumlahan vektor dapat dilihat pada gambar dibawah :

Sifat – sifat penjumlahan vektor adalah sebagai berikut.
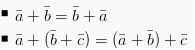
Pengurangan Vektor
Dalam pengurangan vektor, berlaku sama dengan penjumlahan yaitu sebagai berikut:
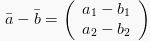
Perkalian Vektor dengan Skalar
Suatu vektor dapat dikalikan dengan suatu skalar (bilangan real) dan akan menghasilkan suatu vektor baru.
Jika v adalah vektor dan k merupakan skalar. Maka perkalian vektor dapat dinotasikan:
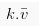
Keterangan:

Secara grafis perkalian ini dapat merubah panjang vektor. Lihat tabel berikut.

Perkalian vektor dengan skalar k dapat dirumuskan sebagai berikut:

Perkalian Skalar 2 Vektor
Perkalian skalar dua vektor dapat disebut juga sebagai hasil kali titik dua vektor, ditulis sebagai berikut:

Contoh Soal:
- Diketahui ada titik A(1, 3, 5), titik B(4, 6, 2), dan titik C(m, n, -5). Apabila titik A, B, dan C segaris maka tentukan nilai p + q !
Pembahasan :
Jika titik – titik A, B, dan C segaris maka vektor AB dan vektor AC bisa juga searah atau berlainan arah.
Sehingga akan ada bilangan m yang merupakan sebuah kelipatan dan bisa membentuk persamaan berikut ini :

Jika B ada diantara titik A dan C, maka
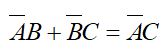
Sehingga
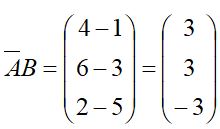

Maka kelipatan m dalam persamaan dapat ditemukan sebagai berikut
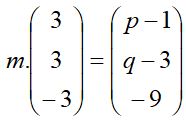
m . (-3) = -9, maka m = 3
Dengan subsitusi nilai m, akan diperoleh:
m . 3 = p – 1, maka p= -8
m . 3 = q – 3, maka q= -6
Jadi,
p + q = – 8 – 6 = – 14
Jawaban: a. -14
2. Diketahui titik A(2,4,6), titik B(6,6,2), dan titik C(p,q,-6). Jika titik A, B, dan C segaris maka tentukan nilai p+q.
Jawaban: b. 24
3. Diketahui ada titik A(2,4,6), titik B(6,6,2), dan titik C(p,q,-6). Apabila titik A, B, dan C segaris maka tentukan nilai p + q !
Daftar Pustaka:
- Emma. 2021. "Vektor (Pengertian, Jenis, Operasi, & Contoh Soal)", https://gurubelajarku.com/vektor/, diakses pada 19 Februari 2021 pukul 06.25 wib.
- Seputarpengetahuan. 2020. "Vektor: Pengertian, Materi, Rumus, dan Contoh Soal", https://www.seputarpengetahuan.co.id/2020/05/vektor.html, diakses pada 19 Januari pukul 06.53 wib.
 dan vektor
dan vektor  bisa juga searah atau berlainan arah. Sehingga akan ada bilangan m yang merupakan sebuah kelipatan dan bisa membentuk persamaan berikut ini :
bisa juga searah atau berlainan arah. Sehingga akan ada bilangan m yang merupakan sebuah kelipatan dan bisa membentuk persamaan berikut ini :





